Fun With Method Missing and C# 4
UPDATE: Looks like the CLR already has something similar to what I did
here. Meet the latest class with a superhero sounding name,
ExpandoObject
Warning: What I’m about to show you is quite possibly an abuse of the C# language. Then again, maybe it’s not. ;) You’ve been warned.
Ruby has a neat feature that allows you to hook into method calls for
which the method is not defined. In such cases, Ruby will call a method
on your class named method_missing. I showed an example of this using
IronRuby a while back when I
wrote about monkey patching CLR
objects.
Typically, this sort of wild chicanery is safely contained within the world of those wild and crazy dynamic language aficionados, far away from the peaceful waters of those who prefer statically typed languages.
Until now suckas! (cue heart pounding rock music with a fast beat)
C# 4 introduces the new dynamic keyword which adds dynamic
capabilities to the once staid and statically typed language. Don’t be
afraid, nobody is going to force you to use this (except maybe me). In
fact, I believe the original purpose of this feature is to make COM
interoperability much easier. But phooey on the intention of this
feature, I want to have some fun!
I figured I’d try and implement something similar to method_missing.
The first toy I wrote is a simple dynamic dictionary which uses property accessors as the means of adding and retrieving values from the dictionary by using the property name as the key. Here’s an example of the usage:
static void Main(string[] args) {
dynamic dict = new DynamicDictionary();
dict.Foo = "Some Value"; // Compare to dict["Foo"] = "Some Value";
dict.Bar = 123; // Compare to dict["Bar"] = 123;
Console.WriteLine("Foo: {0}, Bar: {1}", dict.Foo, dict.Bar);
Console.ReadLine();
}
That’s kind of neat, and the code is very simple. To make a dynamic
object, you have the choice of either implementing the
IDynamicMetaObjectProvider interface or simply deriving from
DynamicObject. I chose this second approach in this case because it
was less work. Here’s the code.
public class DynamicDictionary : DynamicObject {
Dictionary<string, object>
_dictionary = new Dictionary<string, object>();
public override bool TrySetMember(SetMemberBinder binder, object value) {
_dictionary[binder.Name] = value;
return true;
}
public override bool TryGetMember(GetMemberBinder binder,
out object result) {
return _dictionary.TryGetValue(binder.Name, out result);
}
}
All I’m doing here is overriding the TrySetMember method which is
invoked when attempting to set a field to a value on a dynamic object. I
can grab the name of the field and use that as the key to my dictionary.
I also override TryGetMember to grab values from the dictionary. It’s
really simple.
One thing to note, in Ruby, there really aren’t properties and methods.
Everything is a method, hence you only have to worry about
method_missing. There’s no field_missing method, for example. With
C# there is a difference, which is why there’s another method you can
override, TryInvokeMember, to handle dynamic method calls.
What havoc can we wreack with MVC?
So I have this shiny new hammer in my hand, let’s go looking for some nails!
While I’m a fan of using strongly typed view data with ASP.NET MVC, I
sometimes like to toss some ancillary data in the ViewDataDictionary.
Of course, doing so adds to syntactic overhead that I’d love to reduce.
Here’s what we have today.
// store in ViewData
ViewData["Message"] = "Hello World";
// pull out of view data
<%= Html.Encode(ViewData["Message"]) %>
Sounds like a job for dynamic dictionary!
Before I show you the code, let me show you the end result first. I
created a new property for Controller and for ViewPage called Data
instead of ViewData (just to keep it short and because I didn’t want
to call it VD).
Here’s the controller code.
public ActionResult Index() {
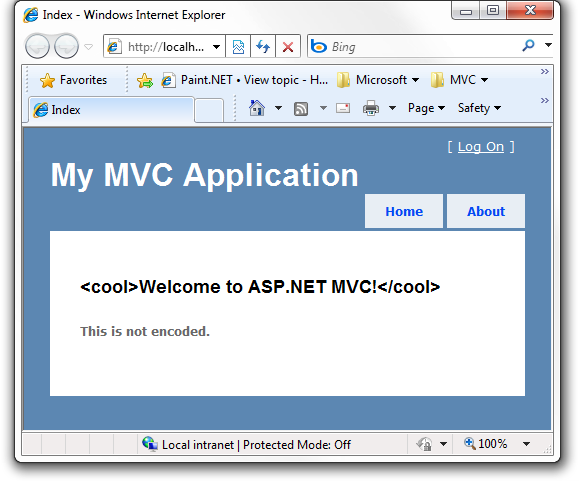
Data.Message = "<cool>Welcome to ASP.NET MVC!</cool> (encoded)";
Data.Body = "<strong>This is not encoded</strong>.";
return View();
}
Note that Message and Body are not actually properties of Data.
They are keys to the dictionary via the power of the dynamic keyword.
This is equivalent to setting ViewData["Message"] = "<cool>…</cool>".
In the view, I created my own convention where all access to the Data
object will be html encoded unless you use an underscore.
<asp:Content ContentPlaceHolderID="MainContent" runat="server">
<h2><%= Data.Message %></h2>
<p>
<%= Data._Body %>
</p>
</asp:Content>
Keep in mind that Data.Message here is equivalent to
ViewData["Message"].
Here’s a screenshot of the end result.
Here’s how I did it. I started by writing a new DynamicViewData class.
public class DynamicViewData : DynamicObject {
public DynamicViewData(ViewDataDictionary viewData) {
_viewData = viewData;
}
private ViewDataDictionary _viewData;
public override bool TrySetMember(SetMemberBinder binder, object value) {
_viewData[binder.Name] = value;
return true;
}
public override bool TryGetMember(GetMemberBinder binder,
out object result) {
string key = binder.Name;
bool encoded = true;
if (key.StartsWith("_")) {
key = key.Substring(1);
encoded = false;
}
result = _viewData.Eval(key);
if (encoded) {
result = System.Web.HttpUtility.HtmlEncode(result.ToString());
}
return true;
}
}
If you look closely, you’ll notice I’m doing a bit of transformation
within the body of TryGetMember. This is where I create my convention
for not html encoding the content when the property name starts with
underscore. I then strip off the underscore before trying to get the
value from the database.
The next step was to create my own DynamicController
public class DynamicController : Controller {
public dynamic Data {
get {
_viewData = _viewData ?? new DynamicViewData(ViewData);
return _viewData;
}
}
dynamic _viewData = null;
}
and DynamicViewPage, both of which makes use of this new type.
public class DynamicViewPage : ViewPage {
public dynamic Data {
get {
_viewData = _viewData ?? new DynamicViewData(ViewData);
return _viewData;
}
}
dynamic _viewData = null;
}
In the Views directory, I updated the web.config file to make
DynamicViewPage be the default base class for views instead of
ViewPage. You can make this change by setting the pageBaseType
attribute of the <pages> element (I talked about this a bit in my post
on putting your views on a
diet).
I hope you found this to be a fun romp through a new language feature of C#. I imagine many will find this to be an abuse of the language (language abuser!) while others might see other potential uses in this technique. Happy coding!
Comments
60 responses