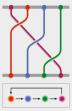Scientific American has a fascinating article this month on Computing with Quantum Knots. In particular, it focuses on using topological properties of a two-dimensionaly confined particles called anyons. Needless to say, the only thing they’ve managed to tie in a knot so far is my brain. But the research is very promising.
I never studied topology in college, though I did try and audit a topology class in Hungary. After a couple classes I decided it was over my head and focused on Number Theory, which is more my thing. Reading this article is spurring a newfound interest.
In essense, one of the difficulties with Quantum computing is that it relies on the superposition states of individual atoms. These states are exceedingly fragile, which make building a real Quantum computer difficult. The benefit of using topological properties is that they are more resistant to change.
The classic example of a topological property is to think of a string in a closed loop. You can twist the and deform the loop all you want, but it retains the same basic topological property of being a loop. You cannot twist or deform it so that it becomes a closed loop with a knot tied in it. You would have to cut it, tie the knot, and then rejoin it, thus changing its topology.
What caught my attention in the article were the number of researches mentioned who are now at Microsoft. The article mentions Michael H. Freedman, Zhenghan Wang, and Alexei Y. Kitaev, all of whom have made advances in the concept of using quantum knots for computation.
The article mentions that these researchers are part of Microsoft’s Project Q. It’ll be interesting to see if Microsoft makes a splash in Quantum computing as it moves forward.